本文在重新审视量子力学和量子测量理论之来龙去脉的基础上，用历史主义的观点认真考察了“测量难题”的渊源和内涵，不仅彻底揭开了它那神秘的面纱，而且为进一步的讨论这个问题明确了目标。
一、第一个难题：测量结果难题
1887年赫兹发现了光电效应，经典物理学的所有观点(无论是波动说还是微粒说)都无法对这一新的现象给予满意的解释。光电效应第一个证明了以牛顿和麦克斯韦等人为代表的经典物理学理论并不总是那么完善。一种新的思想逐渐萌发。
在这种新的思想萌芽里，有人把光的波动性和粒子性统一起来，提出光的“波粒二象性”的说法。在进一步的研究中，科学家把这种想法先推广到电子，后来认为这是所有基本粒子所具有的普遍性质，“在原子和亚原子范围内，粒子和波动之间的严格区别已经失去意义。”[1]这种“量子理论最有代表性的特点”[2]，实质上是一种应用经典物理学概念去理解量子原理的做法，大多数科学家坚决反对这种“二元论”。所以，1923年德布罗意解释电子时，将描述波粒二象性的态函数称为“相位波”。德布罗意相位波实际上只有粒子才是真实的存在，虚拟的非物理场并不携带能量和动量，它只起到引导粒子运动的作用，加载于粒子运动之中。1926年，薛定谔在德布罗意相位波的概念基础上，建立了量子力学方程，将原来的波的含义改造为“物质波”，相应地称自己的理论为物质波理论。这两种解释本质上是微粒说和波动说的翻版，不能令人满意。
1926年德国物理学家玻恩提出态函数的统计诠释，认为波函数Ψ描述的是系统的几率
幅。几率幅是量子力学最重要的基本概念之一，“我们讨论量子力学的观念，······其他的东西······多半都是这一概念的结论”[3]。几率幅提出之后，波粒二象性的二元对立也就彻底消失了，“完全消除了这一表观上的自相矛盾”[4]。正如玛格瑙(Margenau)说：“电子既不是粒子也不是波。”“一个电子是一件抽象的事物，它不再能使用日常经验所熟悉的样子去直觉地理解······”[5]
至此，量子物理学终于找到了适合于自己的独特的基本概念，从而完全摆脱了经典物理学观念的隐蔽，走上了成熟发展的道路。几率波解释虽然平息了微粒与波动表观对立的矛盾，但是它所引发的新的矛盾将比这个矛盾更难调和。几率波解释完全决定了测量结果的性质
——统计性，这就是“测量难题”的第一个难题——统计结果难题。测量结果难题成为“测量难题”最根本的问题。“薛定谔猫论”就是对这个问题的形象描述。由于统计性的结果，我们陷入猫“既死又活”的悖论。
这个难题“难”在什么地方?第一，科学家难以理解更难以回答“为什么微观世界是不确定性的”。到了十九世纪末，经典方案取得的成就给人印象极为深刻，“所有已知的物理现象似乎都能在一个普遍的物质(也就是微粒)和辐射(也就是场)的理论中找到他们的解释”[6]。物理学家悲痛地接受几率波函数的统计本性，“梦想回到牛顿一麦克斯韦的经典格式，······是无望了，是误入歧途和不合时宜的。”[7]但是，这种统计性背后的实在是怎么回事呢?大自然为什么会这样呢?爱因斯坦斥责说：“上帝是不会掷股子的?”第二，对于“这种统计性是系统的统计性还是个体的统计性”这样的问题仍旧长期争论?对该问题的回答存在鲜明对立的两派。有些人认为量子力学的这种统计诠释建筑在对大量测量结果统计平均的基础之上，完全否定对单次测量做出预言，这种观点被统称为“统计解释”。玻恩一开始提出波函数几率诠释时就抱这种观点，爱因斯坦也明确声称：“波函数所描述的无论如何不能是单个系统的状态；它所涉及的是许多个体系······”。[8]与此相反，另一些人认为几率波可以描述个别系统的状态，这种几率观点并不违背拉普拉斯经典概率论，持这种观点的被统称为“非统计解释”。以玻尔为核心的“哥本哈根学派”是这种观点的主要信徒。
总之，“测量难题”的第一个问题源于1926年波函数的几率诠释的提出，测量结果的统计性，也就构成了“测量难题”中最基本的问题。
二、第二个难题：同时性测量难题
回到历史发展的线条继续考察。
1927年，海森堡受爱因斯坦狭义相对论里对“同时性操作”定义的启发，用高斯型波包的例子第一个导出了“测不准原理”[9],当时他称作“不确定关系(uncertainty relation)”。当玻尔看到海森堡的工作时，欣然同意海森堡的结论，但是不满于海森堡没有从波粒二象性着手研究。同年秋天，玻尔在科莫会议上提出互补原理，并且通过波粒二象性的论证重新导出了测不准原理。后来，海森堡从电子单缝衍射实验、自由电子、束缚电子等例子论证测不准原理。实际上，海森堡只是“简单枚举”了测不准原理的实例，并没有给出严格的证明。这时，量子力学的基本数学结构和物理诠释都已建立起来了，人们自然马上尝试在量子力学基本假设的基础上，给出测不准原理的严密推导。这正是解决这一问题的合适途径。
实际上，1927年夏天，海森堡的文章刚刚发表，肯纳德(Kennard)就在一篇评述性文章里采用不确定度的定义，第一次运用量子力学的数学公设证明了对任意态函数Ψ有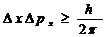
1928年，韦尔(Weyl)在《群论和量子力学》里，首次写进了测不准原理的内容，并在泡利的建议下，使用施瓦兹(Schwarz)不等式进行推导。[10]1929年，罗伯斯坦(Roberston)成功地把韦尔的方法运用到任意两个不对易的力学量，得出一般情况下两个力学量的测不准原理。[11]今天我们看到的实质上就是罗伯斯坦推导的改写。1930年，密切关注事态发展的薛定谔又改进了罗伯斯坦的结果，使之具有严格的形式，终于每年翻出新花样的测不准原理的推导告一段落。
测不准原理描述的是两个不对易的力学量“同时”被测量时，不能同时精确地决定粒子的两个量。测不准原理是“量子物理学中的一个具有创新和革命性的理论，它导致了人们对一些基本的物理概念和哲学思想的认识上的改变”[12]。但是，测不准的原因是什么?这就是“测量难题”的第二个难题——同时性测量难题：我们能确定地得到什么?
当我们尝试着回答上述问题时，感觉到存在以下困难。
第一，测不准原理里的“不确定度”描写多次测量结果的统计散布，还是指单次测量结果的精确度?以哥本哈根学派为首的非统计解释认为，既然态函数可以描述单个系统的状态，那么“不确定度”就能描述单次测量的精确度。然而，早在三十年代，波普尔就在《科学发现的逻辑》一书中，对这种观点提出了责难[13]。从50年代开始沿着这一方向，经过玛格瑙、邦格(Bange)和玻姆(Bohm)等人的努力，对正统解释展开了全面的批评[14]，明确指出该关系只限于多次测量的统计解释。按照统计解释，态函数的模方代表多次测量中测量值出现的相对频率分布，力学量的平均值也指对处于Ψ状态的系统进行多次测量的结果。既然量子力学基本假设原则上不包含对单次测量结果的预言，那么由这些基本假设推演出的测不准原理只能理解成对于态函数描写的量子系统进行多次测量得到的统计散布△A和△B的限制；在单次测量里自然没有统计散布可言。这样一来，这个问题又转移到了第一个难题。
第二，非统计解释认为，单次测量所得到的两个不确定度关系，自然要求每次都能同时测量这两个量，而测不准原理就是同时测量的不确定度的限度。相反，统计解释全然否定这种同时性测量。代表非统计解释的玻尔认为，测不准的原因在于测量过程带了不可控制的干扰：“正是由于不可忽视系统和测量器械的作用，就意味着每一次观察都将引入一个新的不可控制的要素。”[15]这种不可控制不仅仅产生在测量仪器和测量系统之间，甚至海森堡认为观察者本身都是一个不可忽视的因素：“在原子物理学中，······观测者和客体之间的相互作用会对被观测体系引起不可控制的影响，······我们会发现，在很多情况下，同时测量两个不同物理量时总是存在一个不能再提高的精度下限，······即所谓测不准原理······”【16】这就是典型的扰动说，但它并非无懈可击，难免会被以下问题责难：难道宏观领域的测量就没有干扰吗?既然是干扰，什么量参与了这些干扰呢?他们并不能给出令人满意的答复。相反地，而统计解释认为，每一观察量的标准差仅由态函数来决定，它们反映的只是态函数的特征，而与其他各种因素无关。
这就是“测量难题”的第二个问题，1927年与测不准原理相伴而生。统计解释和非统计解释为此进行了永不停息的论战。
三、第三个难题：测量过程难题
我们再一次回到科学发展的历史轨道。
二十年代末，冯·诺伊曼开始对量子力学的理论体系做出公设化的表述，后来他把这些工作总结在《量子力学的数学基础》[17]一书中，成为经典著作。他认为量子力学的形式体系可以由以下五个公设构成的：
公设Ⅰ 每一系统对应有一希尔伯特空间，其矢量(态矢量、波函数)完备地描述了系统的状态。
公设Ⅱ 每个可观察量A唯一地对应于一个作用于希氏空间中的自伴算符。
公设Ⅲ 对于一个处于态中的系统，对可观察量A的一次测量结果处于λ1与λ2：之间的几率PA(λ1，λ2)为∣Eλ1一Eλ2∣，其中E是属于A的恒等分解。
公设Ⅳ 态矢量Ψ的时间演化由方程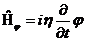
(哈密顿量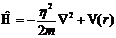
只适应用非相对论性单粒子情况)决定，其中哈密尔顿量
公设Ⅴ 若对可观察量A的一次测量所得的结果在λ1与λ2之间，则系统在紧接着测量之后的态是的Eλ1~Eλ2的一个本征函数。
公设Ⅰ和Ⅱ称为对应公设，它们把原始概念与数学量联系起来，前者规定了使用什么样的基本数学框架描写量子力学里的物理系统，后者规定了如何描述物理世界的一个实在量。这种对应只是一种抽象的理论命题，还没有同经验事实发生什么联系，而这种联系从公设Ⅲ才开始挂上钩。公设Ⅲ是平均值公设，假定力学量的测量值谱就是相应算符的本征值谱，说明量
子力学是统计性质的，对所有的诠释问题都起着至关重要的作用。需要注意的是，这种联系只是一般性的和初步的，因为它规定的力学量测量值的谱，只是一种可能性，还不是具体的现实性，为了了解在确定状态的物理系统的具体性质，还必须知道测量值在规定的谱上是怎样分布的，遗憾的是，公设Ⅲ只对测量结果的平均作了假定，仍然不够具体。其实对单粒子系统来说，以上三条公设实际上已经组成了量子力学的重要的甚至是全部的概念基础。公设Ⅳ是“量子动力学”公设，给出了量子力学的运动方程；对于单粒子系统或者所含粒子都不相同的系统，Ⅰ～Ⅳ已经可以组成一套完整的基本假设。公设V又叫投影假说，刻画了量子测量的过程和性质。
根据冯·诺伊曼第V公设，在接受测量之前，系统处在R的非本征态。通过对R的测量，得到测量值必定是R的某一本征值λｎ，测量之后系统的态变到R的本征值λｎ对应的本征态Ψｎ。换句话说，按上述假设，通过测量系统的态从Ψ变成Ψｎ，也就是说Ψ“投影”到它的一个分量Ψｎ之上。正因如此把这一公设叫做投影公设。因为薛定谔理论中态函数被看成空间存在的真实的波，粒子是波的密集，称为“波包”；相应地，测量前后系统状态的这种变化被称为波包的“编缩”或态矢的“坍缩”。
如此一来，就有新的问题出现了，即“测量难题”的第三个难题——测量过程难题：测量过程中发生了什么?如果真的存在“波包编缩”，波包具体是怎样编缩的?
测量过程难题的难点所在比较明显。第一，波包塌缩给出了测量演化的间断性，导致了逻辑推演上的不完备性和跳跃性，甚至动摇了量子力学的数学基础；第二，如果接受这种间断性，跳跃的具体情况是什么?跳跃的本质是什么?其实没有说清楚。“薛定谔猫论”也是对该问题的最极挑战。在猫论中出现了“既死又活”猫，这仅仅是一个结果，这个结果在测量过程中是怎样从一个统计的预言过渡到一个确定的实在的呢?这正是测量过程难题所要面对的。第三，在量子力学的标准框架中，经典仪器的引入是不可避免的。但是，人们希望量子力学成为描述整个宇宙的一个普遍理论，它不仅能够描述一个微观的物理系统，还应当描述观测着这个系统的宏观测量仪器。这就要求建立一种动力学的量子测量理论：通过仪器和系统的相互作用，把系统和仪器组合的系统看成一个服从量子力学的整体。如此一来，测量过程中产生了量子纠缠，量子纠缠是如何发生的呢?消相干又如何实现?这又和第二个难题缠绕在一起，至今都无明确的答案。
冯·诺伊曼的公设化体系比较抽象，以希尔伯特空间为数学基础又包含了“波包编缩”假设。因而，大多数人倾向于玛格瑙的比较简单明了的一套公设化体系。事实上，绝大多数物理学家认可的也是玛格瑙的体系。对于含有两个或更多全同粒子系统，在冯·诺伊曼的公设化体系中没有假定，在玛格瑙的体系中将上述第V公设改为全同性原理，甚至有人将它改成对称性公设，弥补了冯·诺伊曼假设的不足之处。但是，玛格瑙不足的地方是，在他的理论中并未述及测量过程的性质。而且，由于冯·诺伊曼的工作具有开创性的意义，使得玛格瑙的工作一直受到“遮挡”而不像前者那样声名显赫。
总之，1932年冯·诺伊曼点燃了第三个难题的火炬，七十年来，从来没有人能够熄灭它。反过来想，也许真的是这团火炬鞭策了量子理论的不断前进的车轮。
四、第四个难题：定域性难题
以上我们沿着历史的河流，考察了量子力学成熟的道路上所遗留下的各种测量难题。但是，第一个难题是对某个系统测量结果的考察；第二个难题是对某个系统两个性质的同时考察；第三个难题是对某个系统测量过程的考察。他们涉及到的只有一个系统，如果涉及到两个系统(或者说一个系统的两个子系统的关联)，又会怎样呢?
在经典时代结束以前，人们已经分清两类客体：微粒和场。微粒由牛顿方程决定，每个微粒在任意时刻的状态可以由它的位置和速度(或动量)定域地确定，例如力学和热学的研究；相反，场由麦克斯韦方程决定，场不能定域地分割成类似前者一样的微粒，却可以扩展到空间的一定范围，表现出具有类似波动的特性，例如电磁学和光学的研究。如果量子系统的不同部分会彼此产生影响，即使他们离得很远甚至之间并没有被人们了解的相互作用，那就是非定域性的；否则，就是定域性的。
从历史的视角来看，定域性问题发端于1935年的EPR佯谬。这一年，爱因斯坦、波多斯基、罗森三人联名发表《能认为量子力学对物理实在的描述是完备的吗?》一文，对量子力学体系本身的完备性提出质疑。该文章认为，量子力学要么是非定域的，要么是不完备的。莫尔卡诺夫曾说：“现在许多物理学家认为：EPR佯谬是‘第三朵乌云’，甚至是20世纪的‘第三次风暴’或‘狂飚’，它似乎必然会使我们的时间和空间观念发生根本改变。”[18]
玻尔通过否定微观世界的可分离性否定了EPR的观点，认为量子力学是完备的。玻尔认为，在微观领域，两个粒子是无法分离的，它们的关联永远存在；既然测量对系统产生了一定的影响，它就对整个系统产生影响，两粒子系统中远方的粒子也不能例外，因此“对远距离产生作用”的某种形式是必要的。这种关联性的非定域性被认为是量子过程所展现的自然界的一个固有的事实。
但是，由爱因斯坦和玻尔所点燃的这场战争，其火药味弥散到了整个科研领域直到今天，即“测量难题”的第四个难题——定域性难题：微观世界是定域性的还是非定域性的?从实验上又如何检验?因为不可分离性很难得到实验的证实，所以这场争论纯粹是观念上没有结论的空谈。
二十世纪中期，美国著名物理学家玻姆将EPR中的两粒子的坐标和动量改为不同的自旋分量，使争论有了新的发展。但是仍然停留在哲理性的讨论平台，而真正的突破是60年代中期贝尔(Bell)理论的提出。
贝尔定理与隐变量理论密切相关。量子力学诞生之初，就有过隐变量理论的尝试，认为量子力学的统计性质是一种由更深层次的隐变量决定的表现现象，可是，1932年冯·诺伊曼的名著证明了如果态函数之外存在着隐变量，就不可能与量子力学的基本假设相容。在这一权威的结论面前各隐变量理论很快销声匿迹。1952年玻姆提出冯·诺伊曼的关于隐变量理论的“不可能证明”存在漏洞，并提出了新的隐变量理论，从此展开了新的争论。
在这样的背景下，1964年贝尔提出可以实际检验隐变量解释同通常量子力学孰是孰非的一种方法：一个定域隐变量理论不能重现量子力学的全部预言。这是一个极其重要的理论推断，“它是近30年来，在这个领域的大多数理论和实验研究的主要动力”[19]，使关于量子力学的争论“从理想到现实跨出了决定性的一步”。[20]
贝尔的工作引起了广泛的注意，后来发现贝尔的结论实际上并不依赖于隐变量解释，只需要“定域性”及“可分离性”的基本假定。从70年代开始，各国物理学家完成了10多项检验贝尔不等式的实验工作，其证明与证否各有千秋，这就为该问题从实证的角度考虑增加了难度。
总之，1935年EPR佯谬为难了整个微观世界，它所导引的定域性问题成为量子世界“测量难题”最难解决的问题，即使有了新的实验发展，仍然不能有一个确定的答案。
综上所述，量子理论已经走过了一个多世纪的历程，量子力学也度过了近七十个春秋。然而，量子力学的真正完成仅用了三四年的时间。也正是在这短暂的时间内，量子力学圆满地完成了基本概念的成熟和基本体系的建构；同样地，也正是在这个过程中，“测量难题”相伴而生了。不仅如此，“测量难题”也与量子力学的基本概念和基本公设融为了一体，贯穿于量子力学基本概念和基本原理的始末。
考察历史上所有有关文献，凡是谈及量子测量的不外乎这四个问题，而且往往从一个具体问题“悄悄秘秘地”转移到另一个问题。也正是这种“悄悄秘秘地”转移，让人总是觉得这个领域很神秘，这个“题”很“难”。当然，这个难题的确很难，但是只要明确了这些难题是些什么之后，最起码它不再神秘。
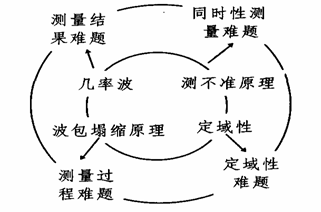
这四个问题的关联是很紧密的，四个问题的每一个问题本身就很复杂，再纠缠在一起就更复杂了。更甚者，他们之间的相互依赖与转移使得四个问题形成了一个怪圈(如下图所示)，永远都找不到哪个问题是产生问题的根本所在。既然抓不住问题的根源，又怎么解决问题呢?在量子世界内，产生这四个问题的几率波、测不准原理、波包塌缩和定域性都是基本概念或基本原理的关键词，无论从哪一个环节入手解决都是棘手的。第一个挑战者玻姆从最基本的数学建构提出隐变量理论，恢复决定性避免波包塌缩，这实际上是从第一个问题入手。第二个多世界解释，建构了多个世界避免波包塌缩，实际上是从第四个问题人手。第三个是模态解释，这是一种机会主义的做法，只想去弥补第三个问题。最后的结果都不是很理想。
要真正地解决测量难题需要做到：(1)继续加强测量理论的研究。事实上，就测量而言，在量子力学基本问题研究中有一块很大的研究领域，称为“测量理论”。在测量理论里，讨论的常常是一些虚拟的“思想实验”或者专门设计来检验某些基本假设的物理实验。但是，“公正地说，物理学家，······很少想过量子力学中的测量理论”。[21]除冯·诺伊曼的《量子力学的数学基础》之外，只有玻姆的名著《量子理论》在最后一编论述过该问题；1957年埃弗雷特提出多世界解释是对测量问题的专门回答；20世纪70年代范·弗拉森提出模态解释，是对该问题的新的理论推导。测量理论是一块尚未成熟且远未取得一致意见的研究领域，进一步加强该领域的物理研究是从物理学本身消解测量难题的最理想的方案。(2)尝试从一个全新的角度诠释量子力学的本质。模态解释所采用的逻辑学与语义学相结合的分析方法将对测量难题的解决提供很好的借鉴价值。也许摆脱物理学传统的思维，将逻辑学的推理演化、语言学形式分析和语义学分析方法等相结合，会得到意想不到的结果。自然，有关这些想法我们将另文阐释。
【参考文献】
[1][德]S．伯朗特、H．塔曼．量子力学图解［M]．陆浩聪，苏清茂译，宇航出版社，1990．1．
[2][美]玻姆．量子理论[M]．侯德彭译，北京：商务出版社．1982，138．
[3]参阅R．P．Feynman，Theory of Foundamental Processes，Benjamin，1962．1．
[4][美]R．P．费曼、A．R．希布斯．量子力学与路径积分[M]．张邦固，韦秀清译，北京：科学出版社，1986．1．
[5]H．Margenau， Fundamental Principles of Quantum Mechanics， in Quantum Theory，I．E1ements，D．R．Batesed，Academic，1961．6．
[6][法]A．梅西亚．量子力学(第一卷)[M］．苏汝铿，唐家镛译，北京：科学出版社，1986．4．
[7]泡利语，见玻恩．我这一代的物理学[M]．侯德彭等译，北京：商务印书馆，1964．181．
[8]爱因斯坦．爱因斯坦文集(第一卷)[M]．许良英等编译，北京：商务出版社，1976．366—367．
[9]W．Heisenberg，Z．Physik，43(1927)，P．172．英译文见E．P．Wingner， Interpretation of Quantum Mechanics， in Quantum Theory and Measurement，J．A．Wheder，W．H．Zurek ed，Princeton，1983．
[10]H．Weyl，the Theory of Group and Quantum Mechanics．Dover．1950．393．
[11]H．P．Roberston，Phys．Rev．，34(1929)，163．
[12][英]阿莱斯泰尔·雷．量子物理学：幻象还是真实[M]．唐涛译，南京：江苏人民出版社，2000．13．
[13]波普尔．科学发现的逻辑[M]．查汝强，邱仁宗译，北京：科学出版社，1986．
[14]雅默．量子力学的哲学[M]．秦克诚译，北京：商务印书馆，1974．24—33．
[15]玻尔．原子物理学和人类知识[M]．郁韬译，商务印书馆，1964．50．
[16][西德]W．海森堡．量子论的物理原理[M]．王正行等译，北京：科学出版社，1983．92．
[17]J．von Neumann， MatheimaticaI Foundations of Quantum Mechanics，Princeton university Press，1955．335．
[18]莫尔卡诺夫．自然科学哲学问题丛刊[J]．1983，(4)：8—14．
[19][英]阿莱斯泰尔·雷．量子物理学：幻象还是真实[M]．唐涛译，南京：江苏人民出版社，2000．47．
[20]关洪．量子力学的基本概念[M]．北京：高等教育出版社，1990．239．
[21][美]E．H．威切曼．量子物理学[M】．复旦大学物理系译，北京：科学出版社，1978．325．
（原载《江西社会科学》2005年第2期。责任编辑：刘清荣）